简介

黑盒测试又叫功能测试、数据驱动测试或基于需求规格说明书的功能测试。该类测试注重于测试软件的功能性需求。
采用这种测试方法，完全不考虑程序内部的逻辑结构和内部特性，只依据程序的《需求规格说明书》，检查程序的功能是否符合它的功能说明。测试工程师无需了解程序代码的内部构造，完全模拟软件产品的最终用户使用该软件，检查软件产品是否达到了用户的需求。黑盒测试方法能更好、更真实地从用户角度来考察被测系统的功能性需求实现情况。

黑盒测试的目的

①、是否有不正确或者遗漏的功能
②、界面是否有误
③、接口上，输入输出是否正确
④、是否有数据结构错误或者外部数据库访问错误
⑤、性能是否满足要求
⑥、初始化或者终止性错误

黑盒测试的优点

①、最大程度满足用户需求
②、相同动作可重复执行，枯燥部分可由机器完成
③、根据测试用例针对性的寻找问题，定位更准确，容易生成测试数据
④、测试直接和程序/系统要完成的操作相关联

黑盒测试的缺点

①、代码得不到测试
②、如果规格设计错误，很难发现
③、测试不能充分进行
④、结果取决于测试用例的设计

设计用例的策略

①、首先进行等价类划分，包括输入和输出条件，减少工作量提高效率
②、边界值分析，发现错误的能力最强
③、错误推断法，补充用例（这个凭经验）
④、对照需求和业务场景逻辑，检查用例
⑤、如果需求说明含有输入条件，设计开始就用到因果图和判定表驱动法
⑥、参数配置类的软件，要用正交实验法
⑦、功能图法，不同时期条件的有效性来设计数据
⑧、业务流清晰的系统，采用场景法

黑盒测试的原则

1、根据需求和规格要求，明确产品要求的正确性
2、针对性的找问题，正确定位
3、根据需求重要性确定测试等级和重点，减少缺陷
4、接口处，输入是否能正确接收，输出是否正确
5、站在用户角度思考，测试

作用

黑盒测试方法着重测试软件的功能需求，是在程序接口上进行的测试，主要是为了发现以下错误。
(1)是否有功能错误，是否有功能遗漏。
(2)是否能够正确地接收输入数据并产生正确的输出结果。
(3)是否有数据结构错误或外部信息访问错误。
(4)是否有程序初始化和终止方面的错误。

测试方法

从理论上讲，黑盒测试只有采用穷举输入测试，把所有可能的输入都作为测试情况考虑，才能查出程序中所有的错误。实际上测试情况有无穷多个，人们不仅要测试所有合法的输入，而且还要对那些不合法但可能的输入进行测试。这样看来，完全测试是不可能的，所以我们要进行有针对性的测试，通过制定测试案例指导测试的实施，保证软件测试有组织、按步骤，以及有计划地进行。黑盒测试行为必须能够加以量化，才能真正保证软件质量，而测试用例就是将测试行为具体量化的方法之一。具体的黑盒测试用例设计方法包括等价类划分法、边界值分析法、错误推测法、因果图法、判定表驱动法、正交试验设计法、功能图法、场景法等。
等价类划分的办法是把程序的输入域划分成若干部分（子集），然后从每个部分中选取少数代表性数据作为测试用例。每一类的代表性数据在测试中的作用等价于这一类中的其他值。该方法是一种重要的，常用的黑盒测试用例设计方法。

划分等价类

等价类是指某个输入域的子集合。在该子集合中，各个输入数据对于揭露程序中的错误都是等效的，并合理地假定：测试某等价类的代表值就等于对这一类其它值的测试.因此，可以把全部输入数据合理划分为若干等价类，在每一个等价类中取一个数据作为测试的输入条件，就可以用少量代表性的测试数据.取得较好的测试结果.等价类划分可有两种不同的情况：有效等价类和无效等价类。
有效等价类：是指对于程序的规格说明来说是合理的，有意义的输入数据构成的集合.利用有效等价类可检验程序是否实现了规格说明中所规定的功能和性能。
无效等价类：与有效等价类的定义恰巧相反。
设计测试用例时，要同时考虑这两种等价类.因为，软件不仅要能接收合理的数据，也要能经受意外的考验.这样的测试才能确保软件具有更高的可靠性。
划分等价类的方法：下面给出六条确定等价类的原则。
①在输入条件规定了取值范围或值的个数的情况下，则可以确立一个有效等价类和两个无效等价类。
②在输入条件规定了输入值的集合或者规定了“必须如何”的条件的情况下，可确立一个有效等价类和一个无效等价类。
③在输入条件是一个布尔量的情况下，可确定一个有效等价类和一个无效等价类。
④在规定了输入数据的一组值（假定n个），并且程序要对每一个输入值分别处理的情况下，可确立n个有效等价类和一个无效等价类。
⑤在规定了输入数据必须遵守的规则的情况下，可确立一个有效等价类（符合规则）和若干个无效等价类（从不同角度违反规则）。
⑥在确知已划分的等价类中各元素在程序处理中的方式不同的情况下，则应再将该等价类进一步的划分为更小的等价类。

边界值分析法

边界值分析是通过选择等价类边界的测试用例。边界值分析法不仅重视输入条件边界，而且也必须考虑输出域边界。它是对等价类划分方法的补充。
（1）边界值分析方法的考虑：
长期的测试工作经验告诉我们，大量的错误是发生在输入或输出范围的边界上，而不是发生在输入输出范围的内部.因此针对各种边界情况设计测试用例，可以查出更多的错误。
使用边界值分析方法设计测试用例，首先应确定边界情况.通常输入和输出等价类的边界，就是应着重测试的边界情况.应当选取正好等于，刚刚大于或刚刚小于边界的值作为测试数据，而不是选取等价类中的典型值或任意值作为测试数据。
（2）基于边界值分析方法选择测试用例的原则：
1）如果输入条件规定了值的范围，则应取刚达到这个范围的边界的值，以及刚刚超越这个范围边界的值作为测试输入数据。
2）如果输入条件规定了值的个数，则用最大个数，最小个数，比最小个数少一，比最大个数多一的数作为测试数据。
3）根据规格说明的每个输出条件，使用前面的原则1）。
4）根据规格说明的每个输出条件，应用前面的原则2）。
5）如果程序的规格说明给出的输入域或输出域是有序集合，则应选取集合的第一个元素和最后一个元素作为测试用例。
6）如果程序中使用了一个内部数据结构，则应当选择这个内部数据结构的边界上的值作为测试用例。
7）分析规格说明，找出其它可能的边界条件。

错误推测法

错误推测法是基于经验和直觉推测程序中所有可能存在的各种错误，从而有针对性的设计测试用例的方法。
错误推测方法的基本思想：列举出程序中所有可能有的错误和容易发生错误的特殊情况，根据他们选择测试用例。例如，在单元测试时曾列出的许多在模块中常见的错误。以前产品测试中曾经发现的错误等，这些就是经验的总结。还有，输入数据和输出数据为0的情况。输入表格为空格或输入表格只有一行. 这些都是容易发生错误的情况。可选择这些情况下的例子作为测试用例。

因果图法

前面介绍的等价类划分方法和边界值分析方法，都是着重考虑输入条件，但未考虑输入条件之间的联系，相互组合等。考虑输入条件之间的相互组合，可能会产生一些新的情况。但要检查输入条件的组合不是一件容易的事情，即使把所有输入条件划分成等价类，他们之间的组合情况也相当多。因此必须考虑采用一种适合于描述对于多种条件的组合，相应产生多个动作的形式来考虑设计测试用例，这就需要利用因果图（逻辑模型）。
因果图方法最终生成的就是判定表。它适合于检查程序输入条件的各种组合情况。
生成测试用例：
(1) 分析软件规格说明描述中，哪些是原因（即输入条件或输入条件的等价类），哪些是结果（即输出条件），并给每个原因和结果赋予一个标识符。
(2) 分析软件规格说明描述中的语义。找出原因与结果之间，原因与原因之间对应的关系. 根据这些关系，画出因果图。
(3) 由于语法或环境限制，有些原因与原因之间，原因与结果之间的组合情况不可能出现. 为表明这些特殊情况，在因果图上用一些记号标明约束或限制条件。
(4) 把因果图转换为判定表。
(5) 把判定表的每一列拿出来作为依据，设计测试用例。
从因果图生成的测试用例（局部，组合关系下的）包括了所有输入数据的取TRUE与取FALSE的情况，构成的测试用例数目达到最少，且测试用例数目随输入数据数目的增加而线性地增加。
前面因果图方法中已经用到了判定表。判定表（Decision Table）是分析和表达多逻辑条件下执行不同操作的情况下的工具.在程序设计发展的初期，判定表就已被当作编写程序的辅助工具了.由于它可以把复杂的逻辑关系和多种条件组合的情况表达得既具体又明确。 [2]

判定表组成法

条件桩（Condition Stub）：列出了问题的所有条件.通常认为列出的条件的次序无关紧要。
动作桩（Action Stub）：列出了问题规定可能采取的操作.这些操作的排列顺序没有约束。
条件项（Condition Entry）：列出针对它左列条件的取值.在所有可能情况下的真假值。 [2]
动作项（Action Entry）：列出在条件项的各种取值情况下应该采取的动作。 [2]
规则：任何一个条件组合的特定取值及其相应要执行的操作.在判定表中贯穿条件项和动作项的一列就是一条规则.显然，判定表中列出多少组条件取值，也就有多少条规则，既条件项和动作项有多少列。
判定表的建立步骤：
①确定规则的个数。假如有n个条件.每个条件有两个取值（0，1），故有2n种规则。
②列出所有的条件桩和动作桩。
③填入条件项。
④填入动作项.等到初始判定表。
⑤简化.合并相似规则（相同动作）。
B. Beizer 指出了适合使用判定表设计测试用例的条件：
①规格说明以判定表形式给出，或很容易转换成判定表。
②条件的排列顺序不会也不影响执行哪些操作。
③规则的排列顺序不会也不影响执行哪些操作。
④每当某一规则的条件已经满足，并确定要执行的操作后，不必检验别的规则。
⑤如果某一规则得到满足要执行多个操作，这些操作的执行顺序无关紧要。

正交试验设计

就是使用已经造好了的正交表格来安排试验并进行数据分析的一种方法，目的是用最少的测试用例达到最高的测试覆盖率。

场景法

软件几乎都是用事件触发来控制流程的，事件触发的情景

便形成了场景，而同一事件不同的触发顺序和处理结果就形成事件流。这种在软件设计方面的思想也可以引入到软件测试中，可以比较生动地描绘出事件触发时的情景，有利于测试设计者设计测试用例，同时使测试用例更容易理解和执行。
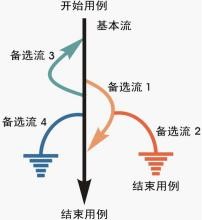
基本流和备选流：如下图所示，图中经过用例的每条路径都用基本流和备选流来表示，直黑线表示基本流，是经过用例的最简单的路径。备选流用不同的色彩表示，一个备选流可能从基本流开始，在某个特定条件下执行，然后重新加入基本流中（如备选流1和3）；也可能起源于另一个备选流（如备选流2），或者终止用例而不再重新加入到某个流（如备选流2和4）。

功能图法

用功能图（流程图）形象的表达操作流（状态迁移图+布尔函数组成）
需要依靠判定表因果图表示逻辑，是黑盒+白盒混合用例的设计方法

例子

1）准备工作
 用Java语言编写一个求一元二次方程的求解程序program1，一元二次方程的系数取整数。
 画出程序program1的控制流图
2）实验内容与步骤
第一步：确定测试策略。在本例中，对被测程序的功能有明确的要求，即：
（1）判断是否组成一元二次方程；
（2）求解两个相等实根；
（3）求解两个不相等实根；
（4）求解虚根；
Public static float Function(int a,int b,int c){

}
写出源程序，并画出控制流图。
第二步：首先用黑盒法设计测试用例，然后用白盒法验证其覆盖性，必要时再进行补充。根据本例的实际情况，可用等价分类法划分输入的等价类，然后用错误推测法作补充。
等价分类法：有效等价类、无效等价类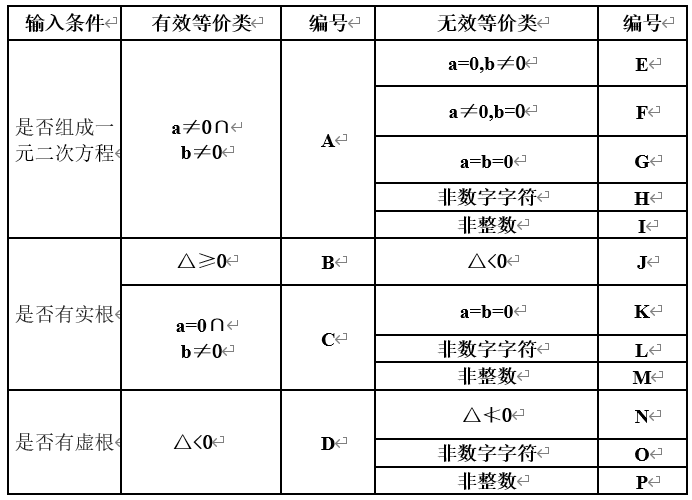

测试用例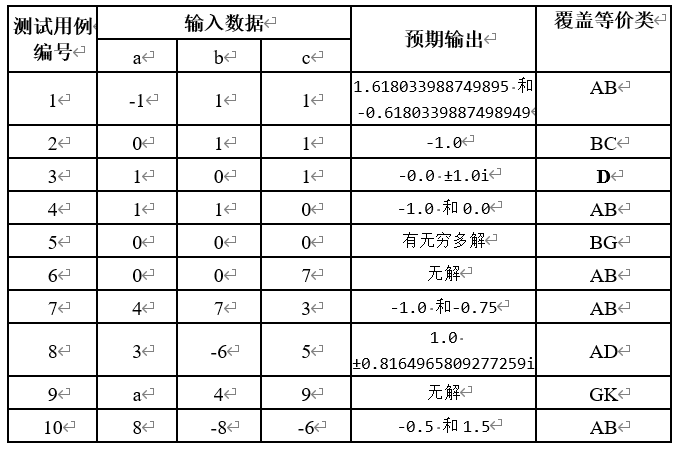

第三步：用白盒法验证第二步产生的测试用例的充分性，看是否满足对被测程序图的完全覆盖。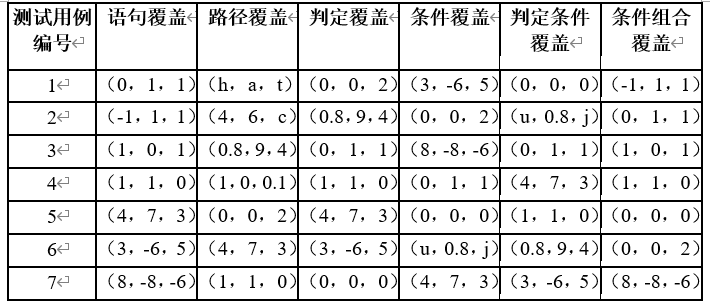

最后，结出结论。

程序：

//求解一元二次方程 ax^2+bx+c=0 的实根和复根， Test类是主类
import java.lang.Math; //math头文件
import java.util.Scanner; //scanner头文件
class OnceBasicQuadraticEquation //求解一元二次方程 ax^2+bx+c 的实根和复根的类，其中 getRoot()方法求根和显示根
{
private double a; //方程的二次项系数
private double b; //方程的一次项系数
private static double c; //方程的常数项 //以上三个成员变量分别是方程的系数
OnceBasicQuadraticEquation() //无参构造方法
{
a = 0;
b = 0;
c = 0;
}
OnceBasicQuadraticEquation(double a,double b,double c) //有参构造方法
{
this.a = a;
this.b = b;
this.c = c;
}
public void setA(double a)
{
this.a = a;
}
public double getA()
{
return a;
}
public void setB(double b)
{
this.b = b;
}
public double getB()
{
return b;
}
public void setC(double c)
{
this.c = c;
}
public double getC()
{
return c;
} //以上六个方法分别对应三个系数的置取方法
public double getDlt() //计算判别式 Δ=b^2-4ac 的值
{
double result = Math.pow(b,2) - 4 * a * c;
return result;
}
private double getRightRoot() //求解右侧较大实根的方法
{
double rightRoot = 0;
rightRoot = (-b + Math.sqrt(getDlt())) / (2 * a);
return rightRoot;
}
private double getLeftRoot() //求解左侧较小实根的方法
{
double leftRoot = 0;
leftRoot = (- b - Math.sqrt(getDlt())) / (2 * a);
return leftRoot;
}
public void getRoot() //求解并显示实根或复根的方法
{
if(a==0)
{
if(b==0)
{
if(c==0)
{
System.out.println(“ 一元二次方程： “ + getA() + “x^2+”+ getB() + “x+” + getC() + “\t 有无穷多解。 “);
//a、b、c 全为零时，定义方程有无穷多解。

}
else
{
//二次项和一次项系数为零，但常数项不为零，方程变为不等式，无解。
System.out.println(“ 一元二次方程： “ + getA() + “x^2+” + getB() + “x+” + getC() + “\t 无解。 “);
}
}
else
{
//二次项系数为零，一次项系数不为零，方程是一次方程，有唯一解。
double result = 0;
result = -getC() / getB();
System.out.println(“ 一元二次方程： “ + getA() + “x^2+” + getB() + “x+” + getC() + “\t 有唯一解： “ + result);
}
} else //二次项系数不为零，方程有两个实根或复根。
{
if(getDlt()==0) //判别式 Δ=b^2-4ac=0，方程有两个相等实根。
{
double result = 0;
result = -getB() / (2 * getA());
System.out.println(“ 一元二次方程： “ + getA() + “x^2+” + getB() + “x+” + getC() + “\t 有唯一解： “ + result);
}
else if(getDlt()>0) //判别式 Δ=b^2-4ac>0 ，方程有两个相异实根。
{
System.out.println(“ 一元二次方程： “ + getA() + “x^2+” + getB() + “x+” + getC() + “\t 有两个实根： “ + getLeftRoot() + “ 和” + getRightRoot());
} else //判别式 Δ=b^2-4ac<0 ，方程有两个复根。
{
//double imaginaryNumber1 = 0;
double imaginaryNumber = 0;
double realNumber = 0;
imaginaryNumber = Math.sqrt(-getDlt()) / (2 * a);
realNumber = -getB() / (2 * a); System.out.println(“ 一元二次方程： “ + getA() + “x^2+” + getB() + “x+” + getC() + “\t 有两个复根： “ + realNumber + “ ±” + imaginaryNumber + “i”);
}
}
}
}
public class Test
{
public static void main(String [] args)
{
double a,b,c;
System.out.println(“请输入参数a b c :”);
Scanner sc = new Scanner(System.in);
a = sc.nextInt();
b = sc.nextInt();
c = sc.nextInt();